问题描述:
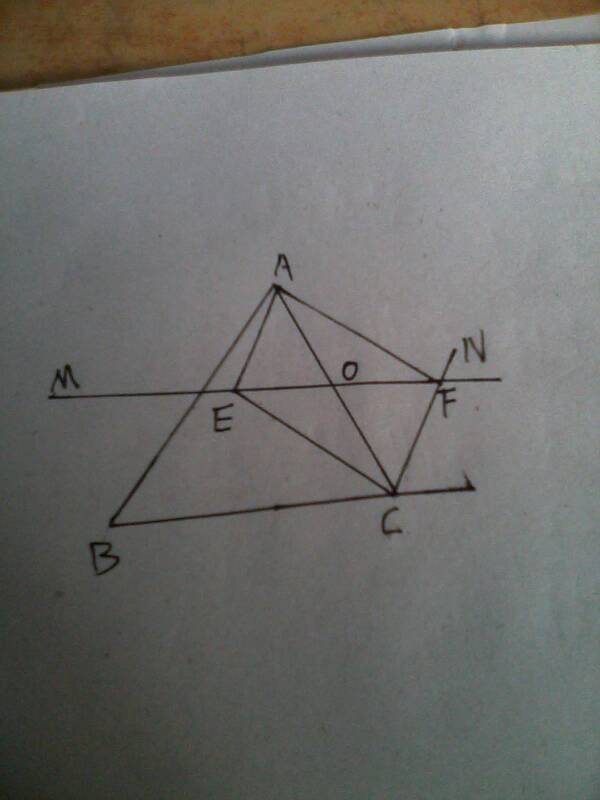
如图,在三角形ABC中,点O是AC边上的一个动点,过点O作直线MN//BC,设MN交角BCA的平分线于点E,交角BCA的外角平分线于点F, (1)求证:EO=FO; (2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论, (3)在(2)的条件下,当三角形ABC满足什么条件时,四边形AECF是正方形?

问题解答:
我来补答展开全文阅读




