问题描述:
如图,在菱形ABCD中,边长为10,∠A=60°.顺次连接菱形ABCD各边中点,可得四边形A1,B1,C1,D1;顺次连接四边形A1,B1,C,D1各边中点,可得四边形A2,B2,C2,D2;顺次连接四边形A2,B2,C2,D2各边中点,可得四边形A3,B3,C3,D3;按此规律继续下去….则四边形A2,B2,C2,D2的周长是(20),;四边形A2013,B2013,C2013,D2013的周长是( )
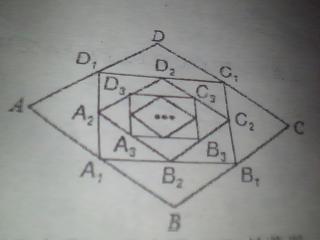

问题解答:
我来补答展开全文阅读


