问题描述:
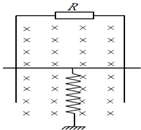
两根足够长的平行光滑导轨竖直固定放置,顶端接一电阻R,导轨所在平面与匀强磁场垂直.将一金属棒与下端固定的轻弹簧的上端拴接,金属棒和导轨接触良好,重力加速度为g,如图所示.现将金属棒从弹簧原长位置由静止释放,则( )
 A. 金属棒在最低点的加速度小于g
A. 金属棒在最低点的加速度小于g
B. 回路中产生的总热量等于金属棒重力势能的减少量
C. 当弹簧弹力等于金属棒的重力时,金属棒下落速度最大
D. 金属棒在以后运动过程中的最大高度等于静止释放时的高度
 A. 金属棒在最低点的加速度小于g
A. 金属棒在最低点的加速度小于gB. 回路中产生的总热量等于金属棒重力势能的减少量
C. 当弹簧弹力等于金属棒的重力时,金属棒下落速度最大
D. 金属棒在以后运动过程中的最大高度等于静止释放时的高度
问题解答:
我来补答展开全文阅读


