三道初三上相似三角形题目 如图RT三角形ABC中,角C=90度,角A的平分线AD交BC边于D,求证AC^2/AD^2=BC/2BD
1.如图,P,Q分别是正方形ABCD的边AB、BC上的点,且BP=BQ,过B点作PC的垂涎,垂足为H,求证,DH垂直HQ
2.如图,在RT三角形ABC中,角C=90度,角A的平分线AD交BC边于D,求证AC^2/AD^2=BC/2BD
3.如图,AD是RT三角形ABC的斜边BC上的高,P是AD的中点,连结BP并延长交AC于E,已知AC:AB=K,求AE:EC的值
有需要可以加分!
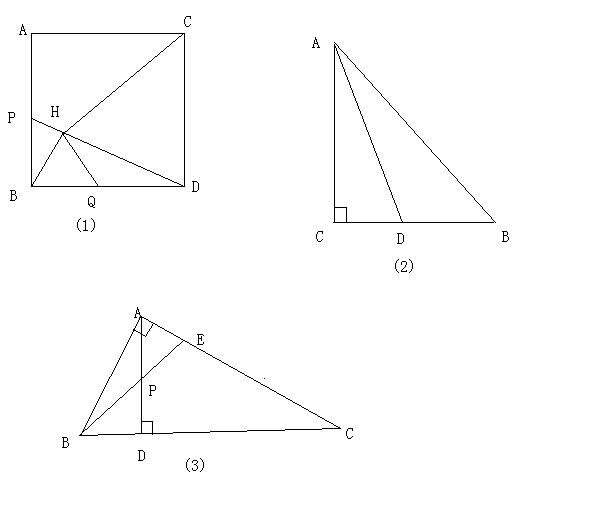
1
证:
∵BH⊥PC
∴在△PBC中,∠PBH=∠BCP
∠CPB=∠BHA
又AB=BC
∴ △ABH≌△BCP
∴ AH=BP
∴ AH=BQ
∴ HDCQ是长方形
因此,DH⊥HQ
2
证:
AC^2/AD^2= cos^2 ∠CAD =(1+cos2∠CAD)/2= 1/2 +cos∠BAC
=1/2 + AC/AB
而 BC/2BD=(1/2)·(BD+CD)/BD= 1/2 +CD/BD
由三角形角平分线定理,有:
AC/CD=AB/BD ;
则 AC/AB = CD/BD;
则:1/2 + AC/AB = 1/2 +CD/BD ;
即
AC^2/AD^2=BC/2BD
这里用到的是三角函数的倍角公式;也可以完全用平面几何的方法如下:
作DE⊥AD;且DE交AC于E;
则 ∠BDE +∠CDA=90度;
而 ∠CAD +∠CDA=90度,则 ∠BDE =∠CAD .
于是又有∠BDE =∠BAD;
∠B共用,因此,△BDE∽△ABD;
则BD/AB=DE/AD;
而明显有:Rt△ACD∽Rt△ADE;
则 DE/AD = CD/AC;
则BD/AB=CD/AC;
→AB/BD=AC/CD ;
→AB/BD +1 =AC/CD +1 ;
→(AB+BD)/BD =(AC+BD)/CD ;
过点D做DF垂直AB于F ∠DFA=∠DFB=90度
因为AD平分∠CAD
所以∠CAD=∠FAD
又∠ACB=∠DFA=90°
AD=AD
所以△ACD全等于△AFD
所以AC=AF CD=CF
因为AC=BC,∠ACB=90°
所以∠ABC=45°
因为∠DFB=90
所以△BFD是等腰直角三角形
所以DF=BF
所以DF=BF=CD
因为AF+FB=AB
AF=AC
CD=DF=FB
所以AC+CD=AB
则:(AB+BD)/BD =AB/CD ;
(AC+2BD)/BD =AB/CD ;
则AC/AE=BC/2BD
而且:AC/AD=AD/AE;
于是有:AC^2/AD^2=(AC/AD)*(AD/AE)=AC/AE;
3
作DF平行BE且交AC于F;
则由此可以得到如下结论:
AP=PD→AE=EF;
而且 EF:EC=BD:BC ;
因此,AE:EC=BD:BC ;
易证明:△ABC∽△DBA∽△DAC ;
由对应边成比例得:
AC:AB=DC:AD=AD:BD ;
即 DC:AD=AD:BD=K;
于是可得到 DC:BD=(DC/AD)·(AD/BD)=K·K =K^2;
则 BD:BC=1/(BC:BD)=1/[(BD+DC):BD]
=1/(1+DC:BD)
=1/(1+K^2);
于是:AE:EC=BD:BC=1:(1+K^2)




